Next: 4 Méthodes de tris Up: Algorithmique Previous: 2 Listes
![]()
![]()
![]()
![]()
![]()
Next: 4 Méthodes de tris
Up: Algorithmique
Previous: 2 Listes
On appelle arbre , la donnée
pour tout noeud n différent de la racine, il existe un noeud n' tel que l'arc (n',n) est un arc.
On dira qu'un arbre est connexe car tout noeud peut être atteint à partir de la racine. Un noeud possède zéro ou plusieurs fils mais possède un et un seul père (excepté la racine).
Les noeuds qui n'ont aucun fils sont appelés feuilles .
On appelle chemin la suite de noeuds
n0n1...nk
telle que
(ni - 1,ni) est un arc, pour tout
i ![]() {1,...,k} .
L'entier k est appelé longueur du chemin
n0n1...nk .
{1,...,k} .
L'entier k est appelé longueur du chemin
n0n1...nk .
Etant donnée un arbre A et un noeud n , le sous-arbre A' de racine n est défini par l'ensemble des fils de n , des fils des fils de n , etc.
La hauteur d'un noeud est la longueur du plus long chemin allant de ce noeud jusqu'à une feuille. La hauteur d'un arbre est la hauteur de la racine.
La profondeur ou niveau d'un noeud est la longueur du chemin allant de la racine jusqu'à ce noeud.
Par exemple, on pourra représenter une expression arithmétique par un arbre dont noeuds sont étiquetés par les opérateurs binaires ou unaires ainsi que les nombres.

Une manière simple de représenter un arbre est d'associer à chaque noeud un enregistrement contenant un ou plusieurs champs pour coder l'étiquette et d'un tableau de pointeurs vers les noeuds fils.
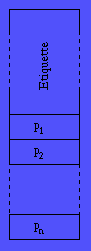
La taille du tableau de pointeurs est donnée par le nombre maximum de fils des noeud de l'arbre. Le ifils d'un noeud est <<pointé>> le le pointeur pi . Cette structure de donnée peut être définie en C comme suit:
struct UN_NOEUD { struct etiquette info; struct NOEUD *tab_fils[MAX_FILS]; }
Un cas particulier des arbres est l'arbre binaire que l'on utilise souvent, par exemple, pour les expressions arithmétiques.
struct UN_NOEUD { struct etiquette info; struct NOEUD *fils_gauche, *fils_droit; }
Le codage des fils d'un noeud par un tableau de pointeurs a un inconvénient: dans les cas où un arbre contient un petit nombre de noeuds ayant beaucoup de fils et beaucoup de noeuds ayant peu de fils, ce codage conduit à consommer beaucoup trop de place mémoire. Une manière de contouner cette difficulté consiste à utiliser un pointeur vers le fils ainée et à chaque fils possèdant un lien vers son frère le plus proche. Cela revient à créer une liste chaîne pour coder la liste les frères.

struct UN_NOEUD { struct etiquette info; struct NOEUD *fils; struct NOEUD *frere; }
L'intérêt des arbres réside dans la facilité de manipluation de cette structure et ce de manière très naturelle en utilsant les fonction récursives.
Les opérations que l'on est souvent amené à effectuer sur les arbres est de l'une des deux formes:
Un exemple type de ce type de manipulation est le parcours pour affichage des expressions numériques en notation préfixé ou postfixé.
void parcours(struct UN_NOEUD *n) { if (n != NULL) { afficher(n-->etiquette info); parcours(n-->fils_gauche); parcours(n-->fils_droit); } }
void parcours(struct UN_NOEUD *n) { if (n != NULL) { parcours(n-->fils_gauche); parcours(n-->fils_droit); afficher(n-->etiquette_info); } }
Pour les arbres binaires et uniquement pour ceux-là, il existe un dernier type de parcours: c'est le parcours infixe. Comme la notation infixée, il s'agit d'effectuer
void parcours(struct UN_NOEUD *n) { if (n != NULL) { parcours(n-->fils_gauche); afficher(n-->etiquette_info); parcours(n-->fils_droit); } }
L'arbre binaire de recherche est une structure de de données particulièrement adaptée pour la gestion d'un ensemble de valeurs sur lequel on veut pouvoir effectuer les opération suivantes:
Un arbre binaire de recherche est une arbre binaire est constitué de telle sorte que l'information figurant à un noeud est plus grande que l'information figurant sur le noeud ``fils gauche'' et est plus petite que l'information figurant sur le noeud ``fils droit''.
Touraivane