Next: 5 Classification des données Up: Le langage C Previous: 3 Structures de contrôle

4 Structure de programmes et fonctions

Dans ce qui suit, on ne s'intéresse qu'au C ANSI: une version moderne et plus propre du langage C originel.

Un programme C est constitué d'un ensemble de fonctions toutes accessibles à partir du programme principal main(). Le découpage en fonction permet de concevoir un programme à partir de briques de base qui sont plus faciles à concevoir, à tester et à modifier.

4.1 Introduction

Avant d'entrer dans le vif du sujet, précisons le vocabulaire que nous allons utiliser dans la suite; ce vocabulaire n'est pas spécifique au langage C mais à tout langage de programmation ``impératif''.

Une fonction est définie par la donnée d'un nom, de ses arguments formels, le type de la fonction (type de l'argument retouné par la fonction) et du corps de la fonction.

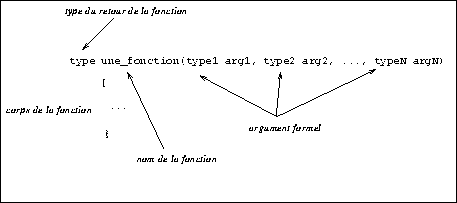
Le corps de la fonction implante la fonction i.e. qu'il précise son comportement. Comme exemple, considérons la fonction qui calcule le pgcd de deux entiers positifs

 unsigned long pgcd(unsigned long x, unsigned long y) \{
    unsigned long r;
    if (x < y) { r = x; x = y; y = x; }
    do {
        r = x % y;           r est le reste de la division entière de x et y
        x = y;              
        y = r;               
    }                        réitérer ce processus en échangeant (x,y) par (y,r) 
    while (r != 0);          tant que le reste de la division entière  x et y est non nul}
    return x;                retourne le pgcd calculé
}

Une définition de fonction ne peut contenir elle-même d'autres défintions de fonctions. Toutes les défintions de fonctions sont au même niveau.

Voici une utilisation de la fonction pgcd définie plus haut.

main() {
     unsigned long a, b;
     printf("Donnez deux entiers\n");
     scanf("%u %u", &a, &b);
     printf("Le pgcd de %u et de %u est %u\n", a, b, pgcd(a, b));
     printf("Le pgcd de 5 et de %u est %u\n", b, pgcd(5, b));
}

Déclarartion de fonction.

On appelle déclarartion d'une fonction la donnée d'un nom, des arguments formels et du type de la fonction. Le corps de la fonction est censé être définie ailleurs (plus loin dans le module ou dans un autre module).

Arguments formels.

Les variables x et y sont les paramètres ou arguments formels de la fonction pgcd. Ce sont bien des arguments formels en ce sens que cette fonction s'applique quelles que soient les valeurs de x et y. Ces valeurs ne seront en fait connues que lors de l'appel de cette fonction.

Arguments effectifs.

Les variables a, b ainsi que la constante 5 sont les paramètres ou arguments effectifs de la fonction pgcd pour cet appel.

Type de la fonction.

Cette fonction retourne une valeur de type unsigned long qui correspond au pgcd calculée par cette fonction. La variable r est une variable locale à la fonction pgcd.

Récapitulatif.

On définit une fonction de la manière suivante:

4.2 Appels de fonctions et gestion de la pile

Une pile (tout comme une pile de linge ou feuille de brouillon) est une structure de données ayant les caractéristiques suivantes: on dépose le dernier élément en haut (on dira sommet) de la pile et le premier élément que l'on utilisera sera le dernier déposé. Une structure de donnée qui possède le comportement que l'on vient de décrire se nomme liste LIFO ou pile (Last In First Out).

Les arguments formels et les variables locales d'une fonction sont stockés dans une zone particulière de la mémoire que l'on appelle segment de pile ou pile ou stack (en anglais).

4.2.1 Le passage par valeur

Lors de l'appel d'une fonction C, le système alloue une portion de la pile dédiée au programme. En simplifiant beaucoup, on peut dire que cette zone mémoire est utilisée pour stocker les arguments, les variables locales automatiques (voir chapitre 5)et l'adresse de retour de la fonction.

Ainsi, à chaque appel de fonction, les arguments effectifs sont recopiés à l'emplacement prévu. On remarque alors que les modifications des arguments formels n'affectent pas les arguments effectifs puisque ces modifications ne sont effectuées que sur des copies des arguments effectifs.

 main() {
   unsigned long a=10, b=15, c;
   c = pgcd(a, b);             fonction définie en page~
    ...
}

Etat initiale.
de la pile juste avant l'appel de la fonction pgcd.

	10	5	0
	a	b	c

Passage de paramètres.
A l'appel de la fonction, recopie des valeurs contenues dans les arguments effectifs (10 et 15)
Allocation de la variable locale r

	10	15	0	@	10	15	0
	a	b	c	@retour	x	y	r

Calcul du pgcd.
Noter que lors de ce calcul les arguments effectifs a et b ne sont aucunement modifiés. Les modifications s'effectuent surdes copies ( x et y ) du contenu de a et b .

	10	15	0	@	5	0	0
	a	b	c	@retour	x	y	r

Retour de la valeur calculée (5)
Restitution de l'espace des arguments effectifs et des variables locales. Au retour de cette fonction, les valeurs de a et b sont inchangées.

	10	15	5
	a	b	c

Cette manière de passer les arguments (par recopie des valeurs des arguments effectifs) se nomme passage d'arguments par valeur. En particulier, dans un passage par valeur les arguments effectifs sont des expressions quelconques: il n'est pas nécessaire que ce soit une lvalue. On peut transmettre par valeurs, des constantes, des expressions complexes constantes, des tableaux, des structures et des unions. Nous verrons dans la section 6.2, le cas particulier des tableaux.

4.2.2 Le passage par adresse

Il est parfois utile de conserver les valeurs calculées par les paramètres formels; c'est l'exemple d'une fonction qui calculerait deux résultats que l'on voudrait récupérer.

Le mécanisme de base en C, c'est le passage par valeur. Pour avoir un passage par adresse, on se contente de passer par valeur l'adresse d'une lvalue. En conséquence, la fonction ne travaille plus sur une copie de la valeur de l'argument effectif mais directement sur celui-ci.

Modifions à présent la fonction pgcd de telle sorte que l'appel de la cette fonction modifie la valeur du premier paramètre effectif.

 
void pgcd(unsigned long *x, unsigned long y) { Noter la présence de 
                                                l'opérateur *  (passage par adresse)
    unsigned long r;
    if (*x < y) {            Noter la présence de l'opérateur *
                              à chaque occurence de x
        r = *x; *x = y; y = *x; 
    }
    do {
        r = *x % y; *x = y;  y = r;              
    }                   
    while (r != 0);          
}

Et l'appel de cette fonction doit se faire de la manière suivante:

 main(){
    unsigned long a=10, b=15;
    pgcd(&a, b);
    ...          
}

Etat initial
Etat de la pile juste avant l'appel de la fonction pgcd

	10	5	0
	a	b	c

Passage de paramètres
A l'appel de la fonction, recopie de l'adresse de a pour x (passage par adresse) et recopie du contenu de b pour y (passage par valeur) Allocation de la variable locale r

	10	15	0	@	&a	15	0
	a	b	c	@retour	x	y	r

Calcul du pgcd.
Noter que lors de ce calcul, pour l'argument formel x , on l'utilise toujours l'opérateur * pour accéder au contenu dans l'argument effectif a . Le comportement de l'autre argument est identique à ce qui est décrit plus haut.

	5	15	0	@	&a	0	0
	a	b	c	@retour	x	y	r

Fin de la fonction.
Restitution de l'espace des arguments effectifs et des variables locales. Au retour de cette fonction, la valeur de b est inchangée; par contre a contient à présent la valeur calculée par la fonction.

	5	15	5
	a	b	c

4.3 Choses diverses

4.3.1 Les fonctions sans argument et/ou qui ne retournent rien

Le mot clé void permer de spécifier que la fonction n'a aucun argument

 int fonction(void) {
     ...
}

L'appel à une fonction sans argument se fait de la manière suivante:

     {
     ...
     i = fonction();   Ne pas oublier les parenthèses !!!
     ...
    }

De même, une fonction qui ne retourne rien (une procédure) se note

 void fonction(...)

4.3.2 Fonctions récursives

En C, les fonctions peuvent être utilisées de manière récursive; c'est-à-dire qu'une fonction peut s'appeler elle-même, soit directement, soit indirectement. Lorsqu'une fonction s'appelle récursivement, chaque niveau d'appel possède son propre jeu de variables automatiques. Le chapitre 1 du polycopié algorithmiqueest entièrement consacré à la récursivité.

Next: 5 Classification des données Up: Le langage C Previous: 3 Structures de contrôle

Touraivane
9/21/1998